原理

二分法以外的快速求根的方法。

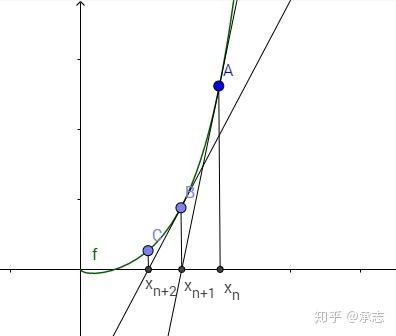
在上图当中，我们要求 $f(x)$ 的根，我们先找到了一个 $x_n$ 点，我们在 $f(x_n)$ 处进行求导取得了它的切线。显然只要这个切线的斜率不为 0，那么我们一定可以获得它和 x 轴的交点。我们将这个交点作为下一个取值，也就是 $x_{n+1}$ 的点。我们重复上述过程进行迭代，很快就可以得到一个足够接近的解。

对于点 $(x_n,f(x_n))$ 处的切线而言，它的斜率是 $f^{'}(x_n)$。它的切线方程很好得到，就是：$y=f^{'}(x_n)(x-x_n)+f(x_n)$。

利用这个方程，可以求到它和x轴的交点，也就是 $x_{n+1}$ 的值为：$x_{n+1}=x_n-\frac{f(x_n)}{f^{'}(x_n)}$，这个式子就是牛顿迭代法的迭代公式，大部分情况下它比二分法的收敛速度要快。

示例

Leetcode 69 题 x 的平方根

题解

// 牛顿迭代法
if (x == 0) {
    return 0;
}
double C = x, xn = x;
while (true) {
    // 这是根据上面公式代入计算得到的
    double xi = 0.5 * (xn + C / xn);
    if (Math.abs(xn - xi) < 1e-7) {
        break;
    }
    xn = xi;
}
return (int) xn;