数学基础
- 如果存在正常数c和$n_0$使得当$N\geqslant n_0$时$T(N)\leqslant cf(N)$,则记为$T(N)=O(f(N))$
- 如果存在正常数c和$n_0$使得当$N\geqslant n_0$时$T(N)\geqslant cf(N)$,则记为$T(N)=\Omega(f(N))$
- $T(N)=\Theta(f(N))$当且仅当为$T(N)=O(f(N))$且$T(N)=\Omega(f(N))$
- 如果对每一正常数c存在常数$n_0$使得当$N>n_0$时$T(N)<cp(N)$,则$T(N)=o(p(N))$。也可简述为,如果$T(N)=O(f(N))$且$T(N)\neq\Theta(f(N))$,则$T(N)=o(p(N))$
ADT
抽象数据类型( abstract data type, ADT )是带有一组操作的一些对象的集合。
表
形如$A_{0},A_{1},A_{2},\ ...,A_{N-1}$的表,表的大小为N
称$A_{i}$后继$A_{i-1}$,$A_{i-1}$前驱$A_{i}$
常用操作
- printList
- makeEmpty
- find 返回某一项首次出现的位置
- insert 从表的某个位置插入某个元素
- remove 从表的某个位置删除某个元素
- findKth 返回(作为参数而被指定的)某个位置上的元素
表的实现
数组
时间复杂度
- printList $O(n)$
- findKth $O(1)$
- insert,remove $O(n)$
链表
为了避免插入和删除的线性开销,实现表的不连续存储
栈ADT
栈(stack)是一个带有限制的表,又叫做LIFO(后进先出)表,它的插入和删除只能在一个位置上进行,即只能在表的末端进行,这个末端叫作栈顶(top)
栈模型
栈的基本操作
push(进栈)等价于一次插入
pop(出栈)是删除最近插入的元素
最近插入的元素在执行pop之前可以通过使用top例程进行考查
对空栈执行pop或top一般均被认为是一个错误,但执行push时空间用尽是一个实现限制,不是ADT错误
栈有时又叫作LIFO(后进先出)表( Last in, First out list )

栈的实现
栈操作是常数时间操作
由于栈是一个表,因此任何实现表的方法都能实现栈
栈的链表实现
使用单链表,通过在表的前端插入来实施push操作,通过删除表前端元素实施pop操作。top操作只是考査表前端的元素并返回它的值。有时也把pop操作和top操作合二为一
栈的数组实现
用到来自vector的back、push back和 pop back,与每个栈相关联的是 theArray和topOfstack,对于空栈它是-1(这就是空栈的初始化做法)。为将某个元素x推入栈中,我们使 topOfStack增1然后置 theArray [topOfstack]=x。为了弹出栈元素,我们置返回值为 theArray [topOfstack],然后使 topOfStack减1
应用
平衡符号
编译器检查程序的语法错误
做一个空栈。读入字符直到文件尾。如果字符是一个开放符号,则将其推入栈中。如果字符是一个封闭符号,则当栈空时报错。否则将栈元素弹出。如果弹出的符号不是对应的开放符号,则报错。在文件尾,如果栈非空则报错。
后缀表达式
$4.99*1.06+5.99+6.99*1.06$
该例的典型计算顺序可以是将4.99和1.06相乘并存为$A_1$,然后将5.99和$A_1$相加,再将结果存入$A_1$;我们再将6.99和1.06相乘并将答案存为,最后将$A_1$和$A_2$相加并将最后答案放入$A_1$。可以将这种操作顺序书写如下:
$4.99\ 1.06*5.99+699\ 1.06*+$
这个记法叫作后缀记法(postfix notation)记法或逆波兰记法(reverse Polish notation)
计算这个问题最容易的方法是使用一个栈。当见到一个数时就把它推入栈中;在遇到一个运算符时该运算符就作用于从该栈弹出的两个数(符号)上,再将所得结果推入栈中。
计算一个后缀表达式花费的时间是$O(N)$
中缀到后缀的转换
当读到一个操作数的时候,立即把它放到输出中。但运算符并不立即输出,而是必须先存在某个地方。正确的做法是将已经见到的运算符放进栈中而不是放到输出中。当遇到左圆括号时也要将其推入栈中。计算从一个空栈开始。
如果见到一个右括号,那么就将栈元素弹出,将弹出的符号写出直至遇到一个(对应的)左括号为止,但是这个左括号只被弹出并不输出。
如果见到任何其他的符号[如+、*、( ],那么我们从栈中弹出栈元素直到发现优先级更低的元素为止。有一个例外:除非是在处理一个)的时候,否则我们绝不从栈中移走(。对于这种操作,+的优先级最低,而(的优先级最高。当从栈弹出元素的工作完成后,我们再将运算符压入栈中。
最后,如果读到输入的末尾,则将栈元素弹出直到该栈变成空栈,再将这些符号写到输出中。
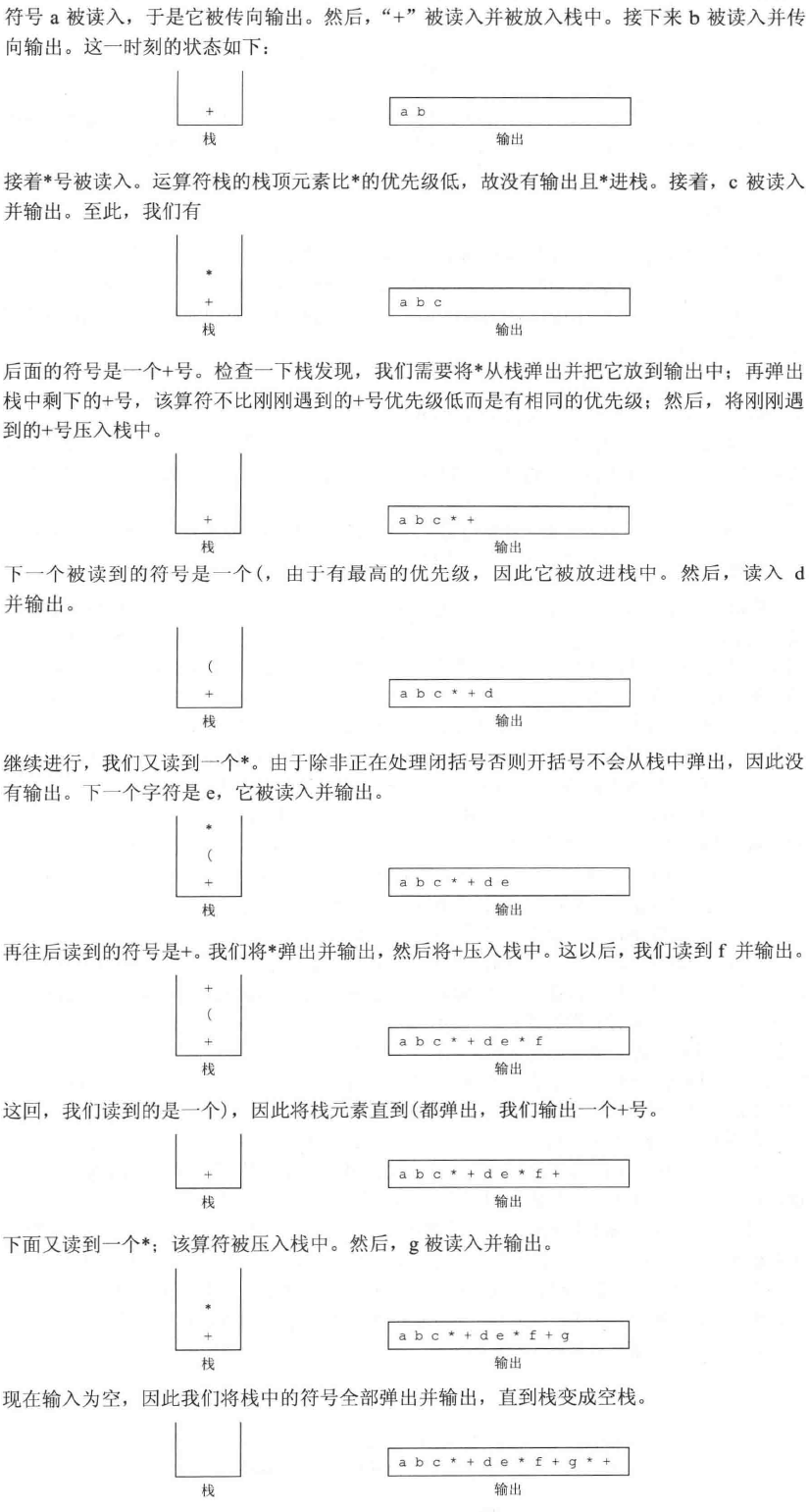
例子:
$a+b*c+(d*e+f)*g$
转换为$abc*十de*f+g*+$
函数调用
尾调用
尾调用优化 - 阮一峰的网络日志 (ruanyifeng.com)
尾递归
传统的递归过程就是函数调用,涉及返回地址、函数参数、寄存器值等压栈,如果递归链过长,可能会 stack overflow
函数在尾位置调用自身(或尾调用本身的其他函数等等),则称这种情况为尾递归
编译器检测到一个函数调用是尾递归的时候,它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点,因为递归调用是当前活跃期内最后一条待执行的语句,于用返回时栈帧中并没有其他事因此也就没有保存栈帧的必要。覆盖当前的栈帧而不是在其之上重新添加一个,这样所使用的栈空间就大大缩减了,这使得实际的运行效率会变得更高。
c++有尾递归优化,而Java没有,建议最好不要使用尾递归
队列ADT
像栈一样,队列(queue)也是一种表。然而使用队列时插入在一端进行而删除则在另一端进行。
队列模型
队列的基本操作是 enqueue(入队),它是在表的末端(叫作队尾(rear))插入一个元素,以及 dequeue(出队),它是删除(并返回)在表的开头(叫作队头( front))的元素。

队列的数组实现
对于每一个队列数据结构,我们保留一个数组 theArray以及位置 front和back,它们代表队列的两端。我们还要记录实际存在于队列中的元素的个数 currentsize。
为使一个元素x入队(即执行 enqueue),我们让 currentsize和back增1,然后置 theRay[back]=x。若使一个元素 dequeue(出队),我们置返回值为theArray[ front],且 currentsize减1,然后使 front增1。
只要front或back到达数组的尾端,它就又绕回到开头。这叫作循环数组(circular array)实现。
队列的应用
称为排队论( queueing theory)的整个数学分支处理用概率的方法计算用户预计要排队等待多长时间才会得到服务、等待服务的队伍能够排多长,以及其他一些诸如此类的问题。
