数据库设计的问题

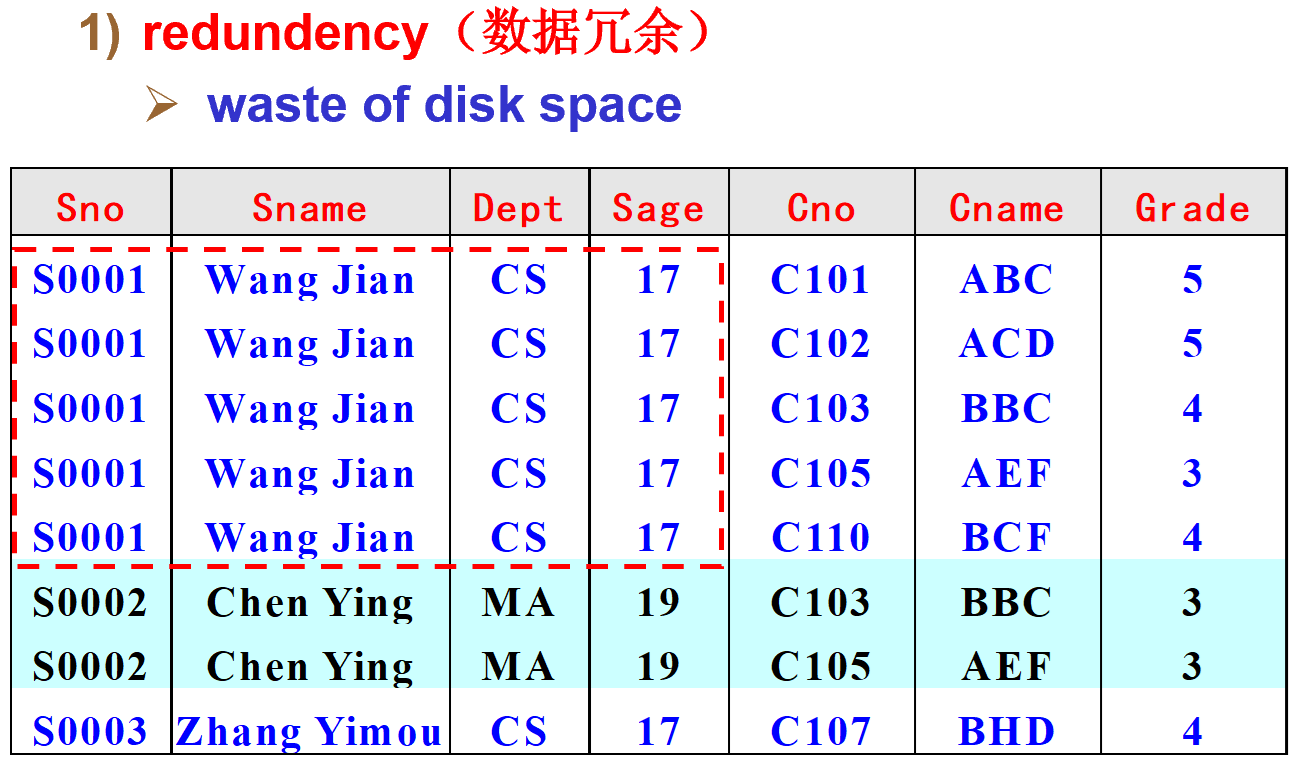
数据冗余：大量重复数据

1. 浪费磁盘空间
2. 不分表，则会导致大量的数据冗余

修改异常

1. 修改异常浪费时间，并且用户容易造成错误。
2. 在修改一个数据的时候，会导致大量数据列的修改。

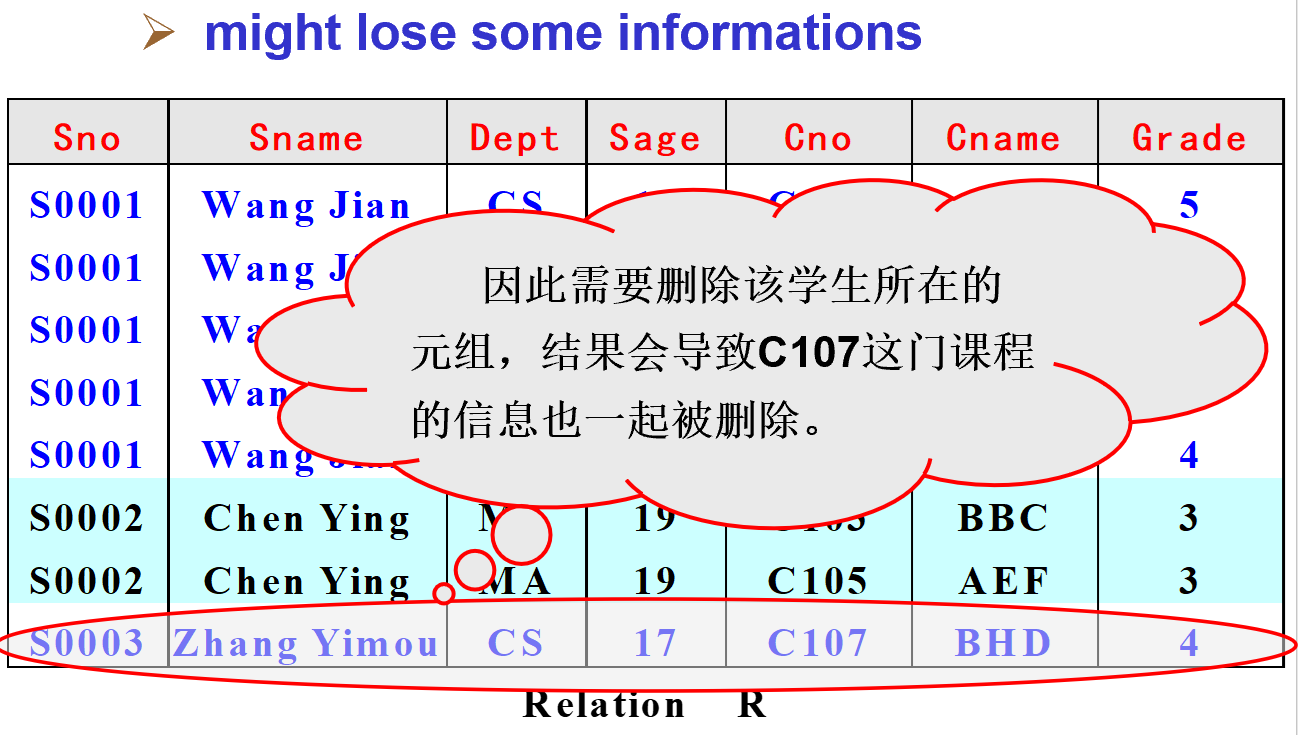
删除异常

删除一个信息实体的同时，可能会导致其他实体信息被同时删除。

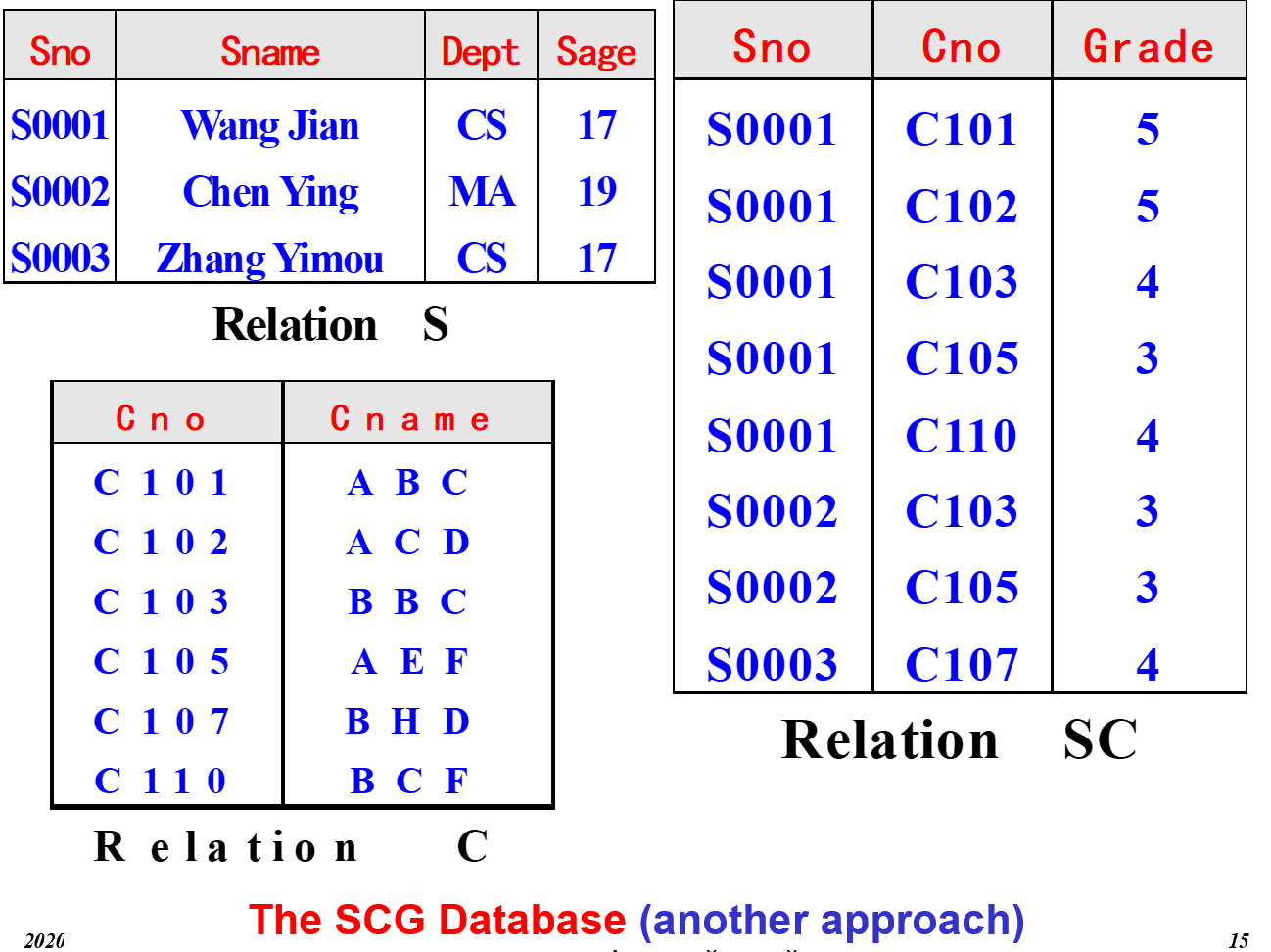
插入异常

实体不完全是无法进行插入的

实体关系模型(Entity-Relationship, E-R)

E-R 模型是一种描述数据库的抽象方法。

实体关系建模的方法更多依赖于直觉而非机器, 但会导致相同的设计。

模型的组成

实体

• 实体是具有公共属性的可区分的现实世界对象的集合。
• 一个实体对应一个关系表，是一组物体。
• 每一行都是一个实体，或者一个实体的实例，代表一个物体。
• 实体是用长方形表示的。

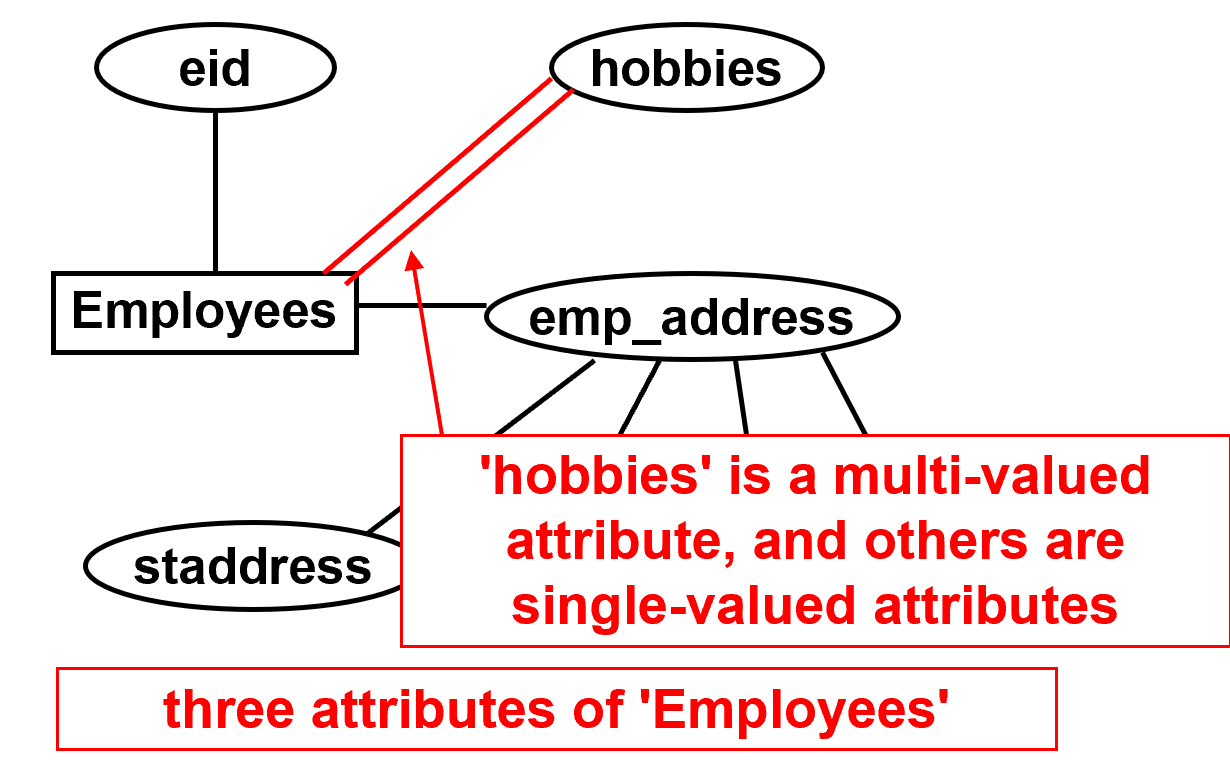
属性

• 属性是描述实体或关系（定义如下）的属性的数据项。

• 属性是椭圆形表示，单值属性用单实线连接，多值属性用双实线连接

  

• 特殊的属性

  • 候选键/标识符：标识符是唯一标识实体实例的属性或属性集，在名字下面用下划线表示。
  • 主键/主标识符：被数据库设计者选择出来的作为表中特定行唯一标识符的候选键，在名字下面用下划线表示。
  • 描述符：描述符是一个非键属性。

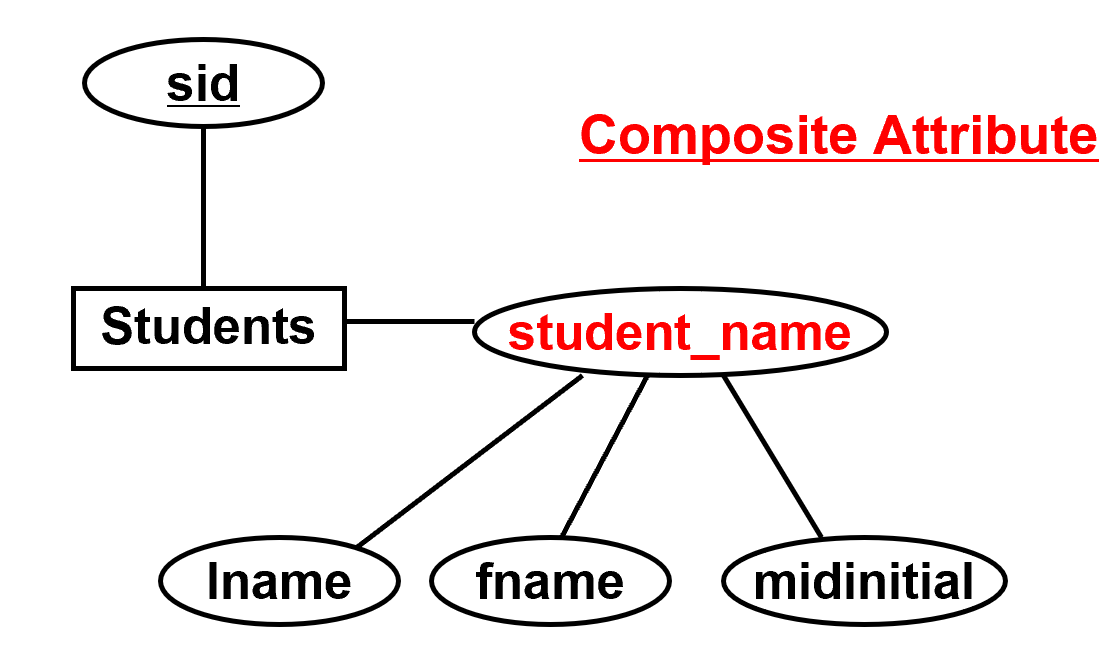
  • 复合属性：一组共同描述属性的简单属性，student_name 是复合属性，符合属性使用单值和多值属性复合而成。

    

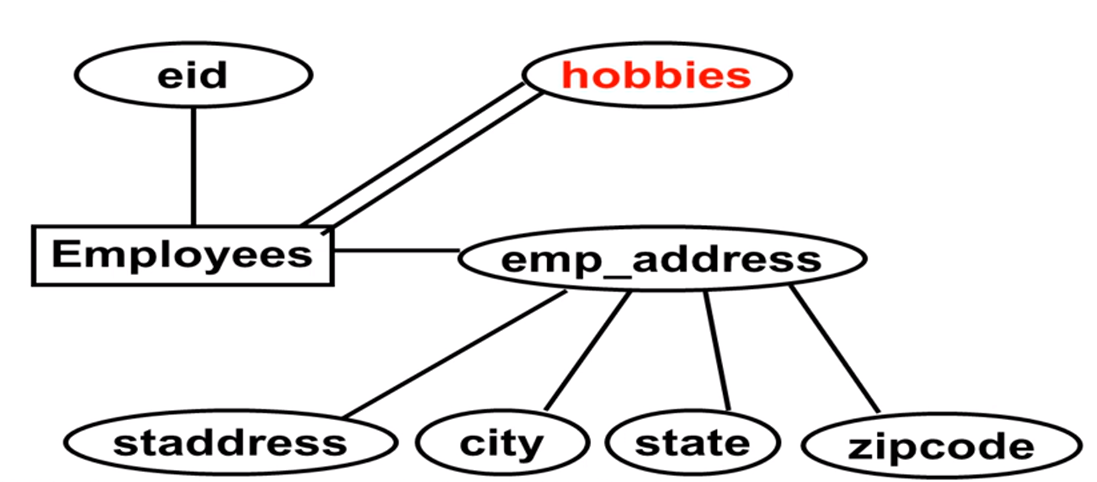
  • 多值属性：单个实例这个属性可以具有多个值。

    

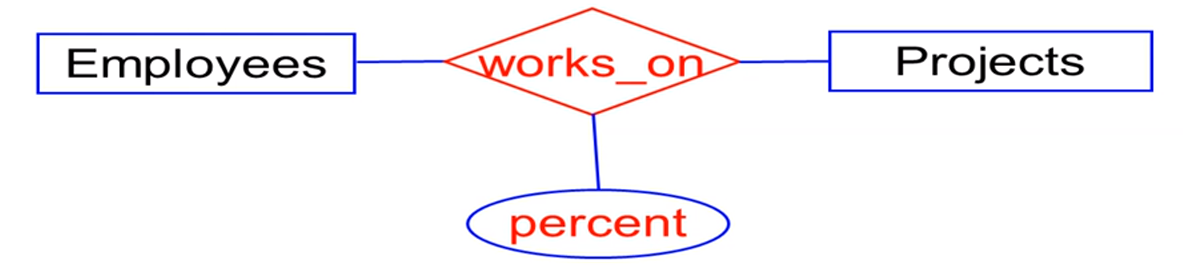
关系

给定 m 个实体的有序列表，分别为 E1，E2，…Em，(同一实体在列表中可能出现多次)

关系 R 定义了这些实体的实例之间的对应规则。

具体来说，R 代表一组 m 元组，这是实体实例的笛卡尔积的子集。

关系是用菱形表示的

关系可以有额外的属性

关系可以有环出现

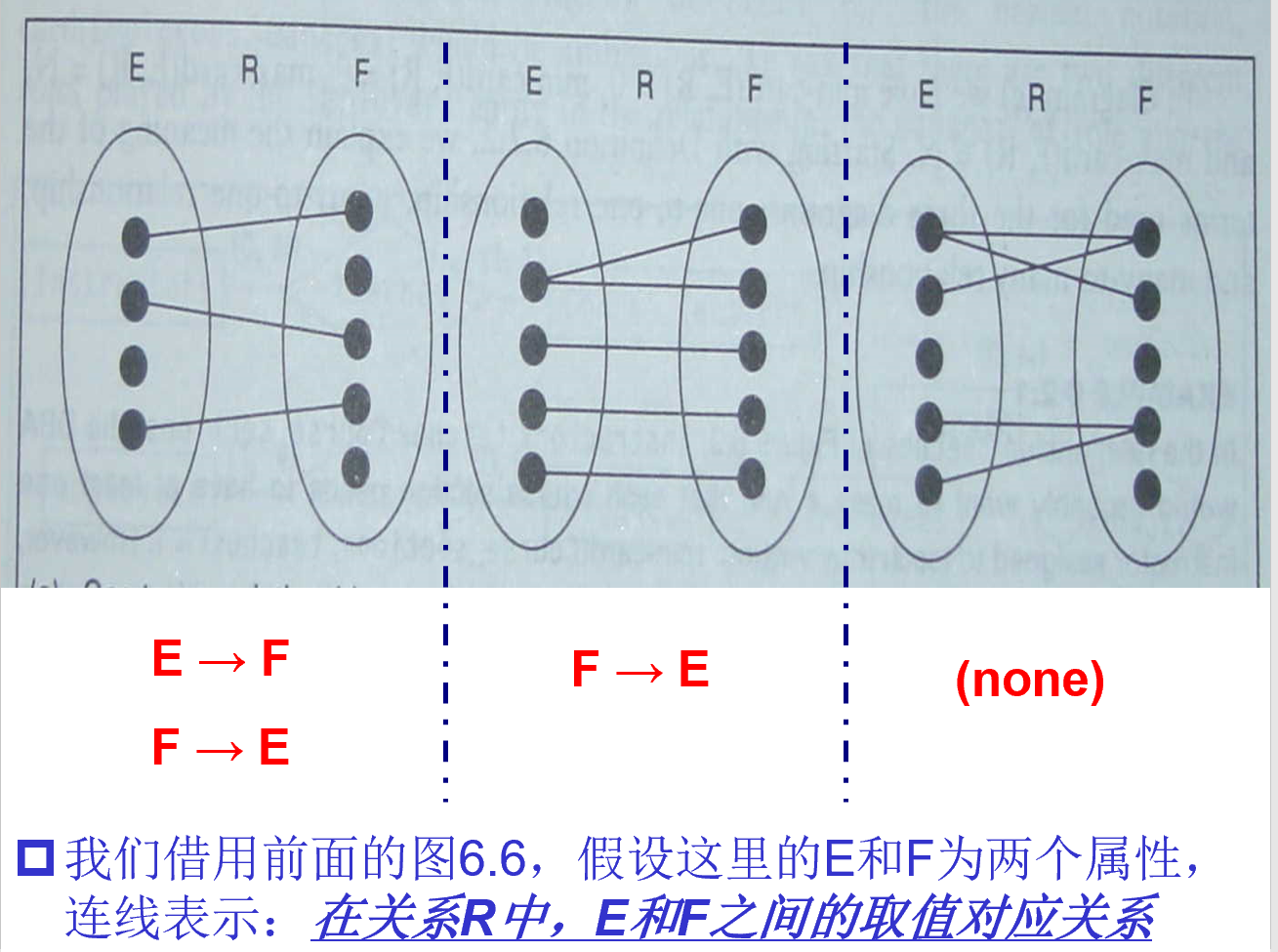
实体参与关系的基数

实体 E 和 F，关系 R，下图中点是实体的实例，线是关系实例

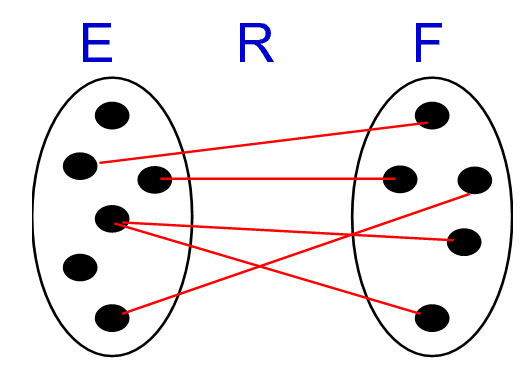
只有如上这四种情况：

• 如果实体 E 中的所有实例最多只有一个关系相关，则 max-card(E, R) = 1
• 如果实体 E 中的所有实例有超过一个关系相关，则 max-card(E, R) = N
• 如果实体 E 中所有实例最少只有一个关系相关，则 min-card(E, R) = 1
• 如果实体 E 中所有实例中有没有关系相关的，则 min-card(E, R)= 0

card(E, R)

每一个关系都有这样的一组 card(E, R) = (0, N)=(min-card(E, R), max-card(E, R))

max-card()

• max-card(X, R) = 1：单值参与
• max-card(X, R) = N：多值参与

min-card()

• min-card(X, R) = 1：强制参与
• min-card(X, R) = 0：可选参与

ER 模型的转换规则

转换规则一

1. 实体映射到单个表。实体的单值属性映射到列(复合属性映射到多个简单列)。
2. 实体出现成为表的行。

转换规则二

1. 多值属性必须映射到其自己的表。
2. 对于ORDBMS 并不适用。

转换规则三(多对多关系规则)

1. 将二元联系转换为关系（N-N关系）：当两个实体E和F参与多对多二进制关系R时，该关系将映射到相关关系数据库设计中的代表表 T。
2. T还包含附加到关系的所有属性的列。

转换规则四(多对一关系规则)

1. 在具有单值参与的实体（多面）中用外键表示。
2. 如果max-card(F, R) = 1，每一个对应关系可以用外键来关联。

转换规则五(一对一关系规则，一侧可选参与)

1. 表示为两个表的外键列在一个具有强制参与的表中：定义为NOT NULL的列。

转换规则六(一对一关系规则，双侧必选参与)

1. 永远不会分裂。 将其视为单个表中的两个实体是适当的。

规范化

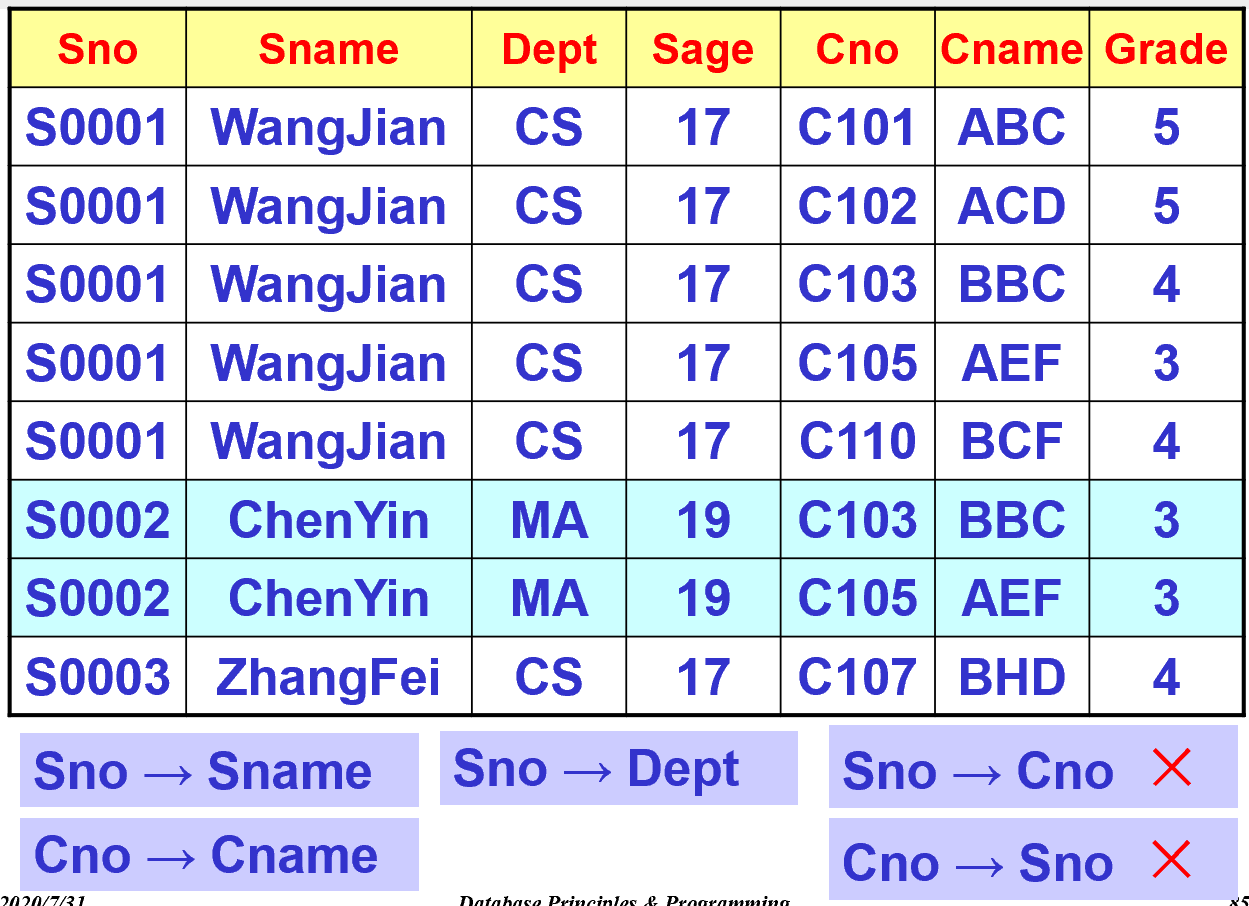
函数依赖(FD, Functional Dependency)

A→B：A 在函数上决定 B，或者 B 在功能上取决于 A。

Armstrong 公理

从已知的一些函数依赖，可以推导出另外一些函数依赖，这就需要一系列推理规则。

基本规则

1. 自反规则：If Y 包含于 X，then X -> Y
2. 传递规则：If X -> Y，Y -> Z，then X -> Z
3. 增广规则：If X -> Y，XZ -> YZ

扩展规则

1. 合并规则：If X -> Y and X -> Z，then X -> YZ
2. 分解规则：If X -> YZ，then X -> Y，and X -> Z
3. 伪传递规则：If X -> Y，and WY -> Z，then XW -> Z
4. 聚集规则：If X -> Y，and WY -> Z，then XW -> Z

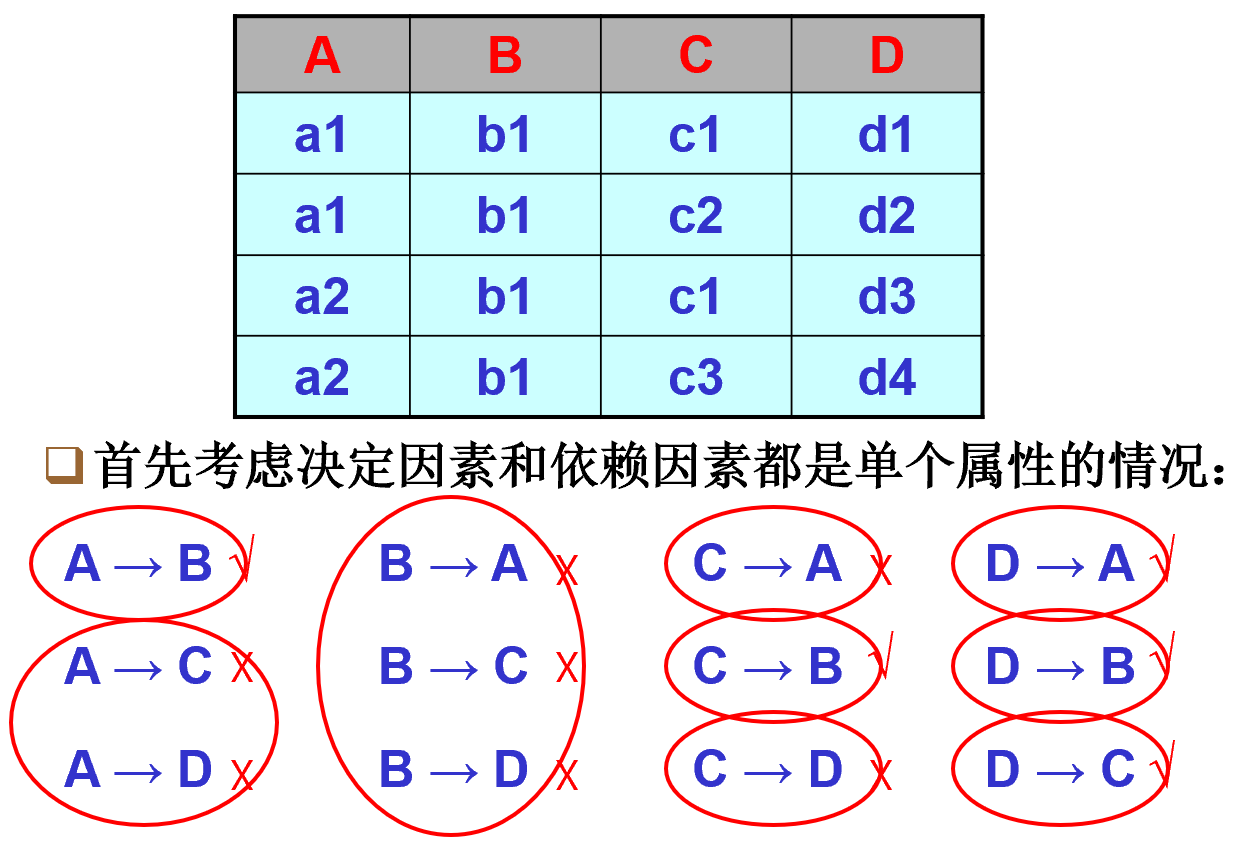
在表格上寻找最小依赖

1. 寻找单个的最小依赖

   

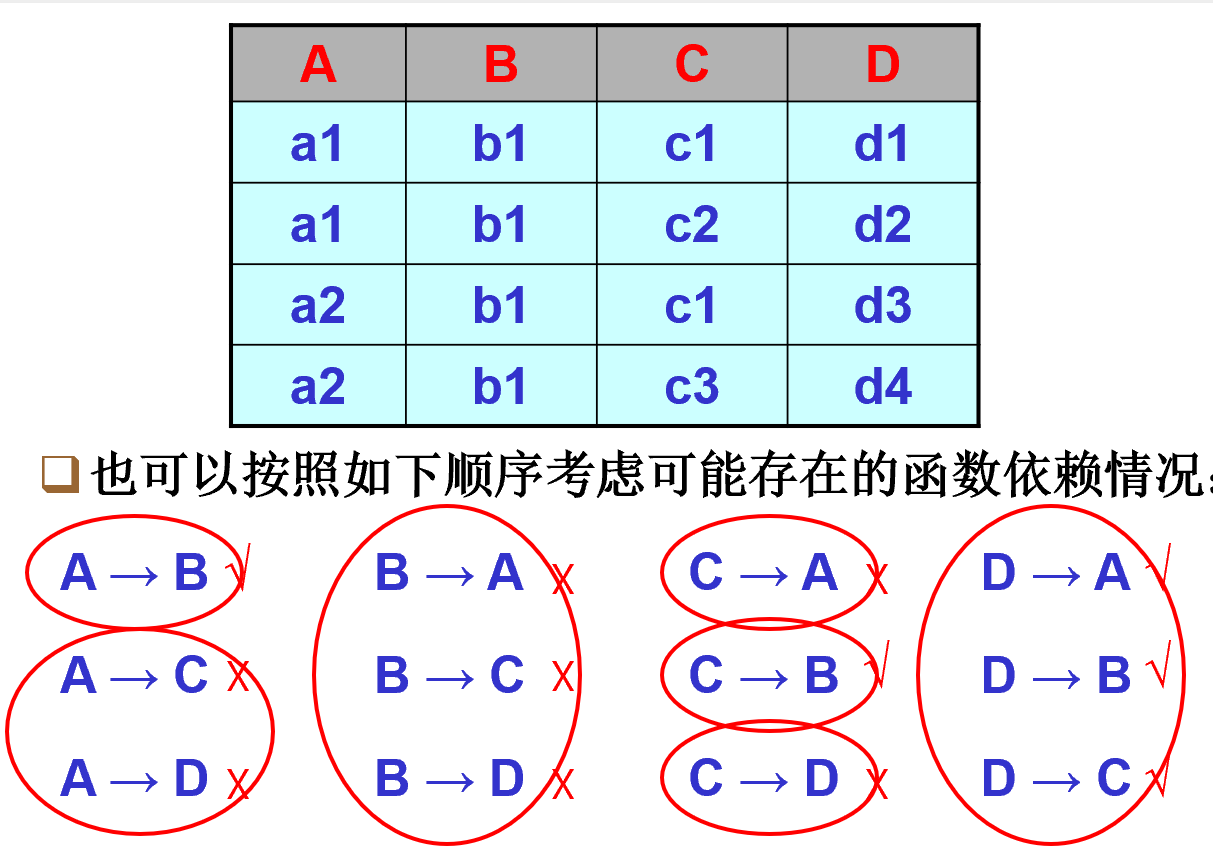
2. 将可以合并的依赖进行合并

   

3. 考虑需要考虑的多种依赖

   

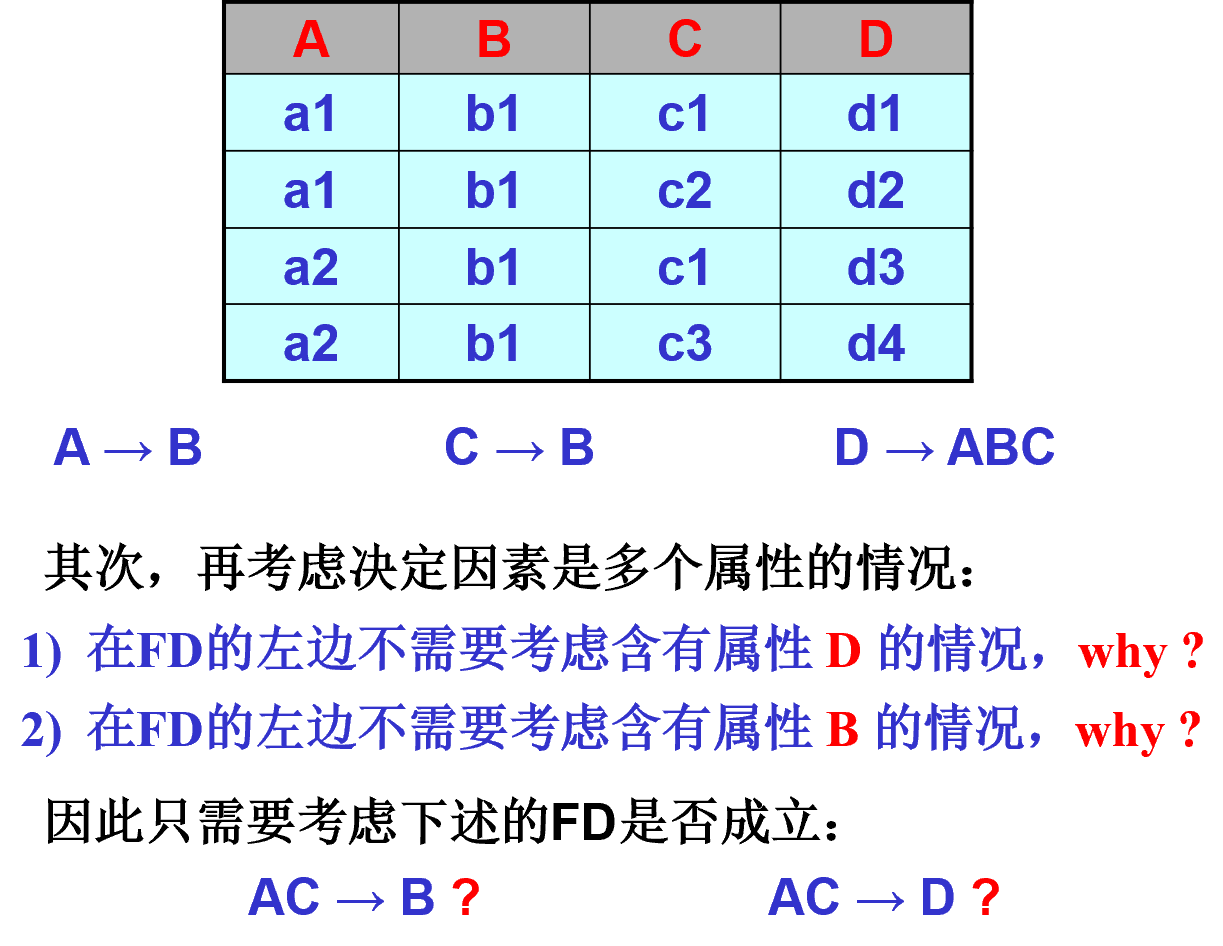
   1. 不需要考虑含有属性 D 的情况是因为 D 决定了剩余所有属性，再增加属性同样能决定剩余所有属性，因为寻找最小依赖所以不需要再增加属性。
   2. 不需要考虑含有属性 B 的情况是因为其它所有属性都决定 B，因此在函数决定关系的左边添不添加 B 并不影响该关系。

4. 考虑最后一个依赖

   

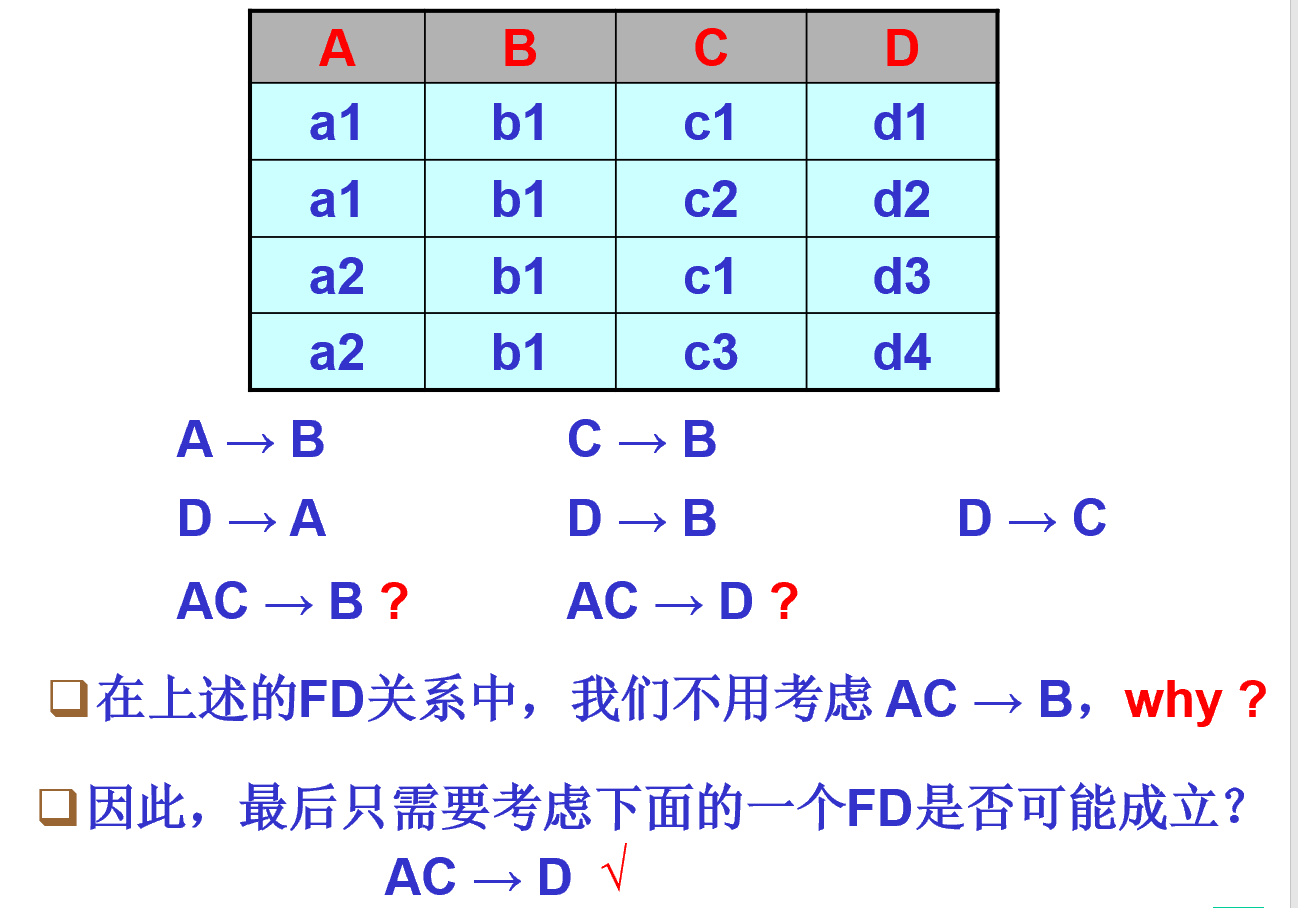
5. 最终的结果

   

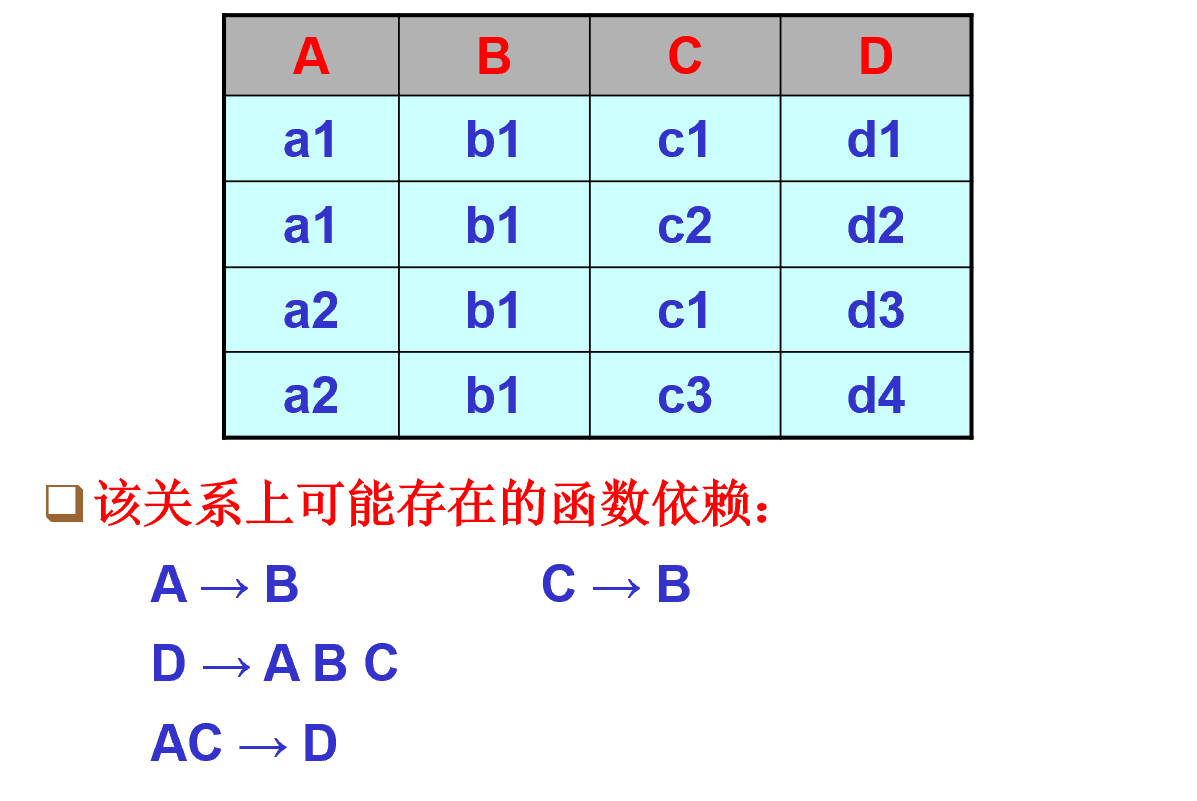
函数依赖集F的闭包(Closure of a Set of FDs)

闭包，记作 $F^+$，就是当前集合能扩展出来的所有的函数依赖集

函数依赖集的覆盖

表 T 上的函数依赖集 F 覆盖了表 T 上的函数依赖集 G 当且仅当 F 可以通过推导关系推导出 G，也就是 G 包含于 $F^+$

函数依赖集的等价：F 覆盖 G 并且 G 覆盖 F

属性集的闭包(Closure of a Set of Attributes)

给定表 T 上的一个属性集合 X，表 T 上的一个属性集合 F ，我们定义 X 在 F 下的闭包(我们记为 $X^+$ 或者是 $X^+_F$ )是在函数依赖集 F 的闭包上的 X->Y 的属性 Y 的最大集合。

$$ X^+_F=\{A|X \rightarrow A \in F^+ \} $$

方法

先把 $X^+$ 赋值为 X，然后对于函数依赖集 F 中的每一项, 若左侧包含于当前的 $X^+$，将右侧的并入 $X^+$，直到 $X^+$ 中不再增加。

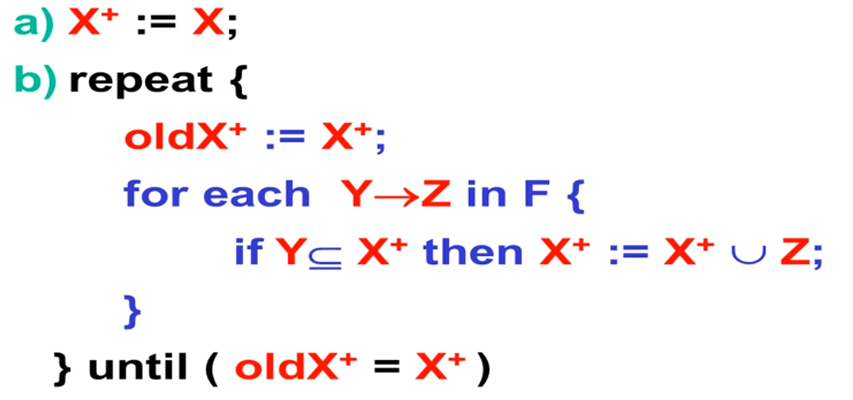
例题

$$ \text { Example 6.6.7: } \mathrm{F}=\left\{\left(\mathrm{f}_{1}\right) \mathrm{B} \rightarrow \mathrm{CD}, \quad\left(\mathrm{f}_{2}\right) \mathrm{AD} \rightarrow \mathrm{E}\right. \text { , } \left.\left(f_{3}\right) B \rightarrow A\right\}, \text { compute }\{B\}^{+} ? $$

答案：

$X^+=\{ A,B,C,D,E\}$

最小覆盖(Minimal Cover)

• 最小依赖也就是最小覆盖，上面是通过表格得到最小依赖，这里是通过函数依赖集获得最小依赖。
• 没有冗余的函数依赖。
• 每一个函数依赖的左边都没有多余属性。

方法

1. 创建函数依赖集 F 的等价函数依赖集 H，它的右边只有单个属性。
2. 顺次去掉 H 中非关键的单个依赖。
   将 H 中的一项 X->Y 去掉，得到新的函数依赖集 J，若 $J^+=H^+$ 则称这个函数依赖是非关键的，也就是说去除这个函数依赖对 $H^+$ 没有任何影响。也可以通过判断 $X^+$ 是否还包含 Y 来判断。
3. 在不改变 $H^+$ 的前提下, 将 H 中的每个函数依赖用左边属性更少的函数依赖替换。
   注意: 第三部中函数依赖集如果发生了变化, 需要返回第二步。
4. 用合并规则创建一个等价的函数依赖集 M。

例题

$F=\{a \rightarrow b, bc \rightarrow d, ac \rightarrow d\}$，求 F 的最小覆盖 M

1. 本来就做好了

2. 依次尝试去掉非关键依赖

   1. 尝试去掉 $a \rightarrow b$，$G=\{bc \rightarrow d, ac \rightarrow d\}$，$\{a\}^+_G=\{a\}$，不包含 b ，所以不能去掉。
   2. 尝试去掉 $bc \rightarrow d$，$G=\{a \rightarrow b, ac \rightarrow d\}$，$\{b,c\}^+_G=\{b,c\}$，不包含 d ，所以不能去掉。
   3. 尝试去掉 $ac \rightarrow d$，$G=\{a \rightarrow b, bc \rightarrow d\}$，$\{a,c\}^+_G=\{a,b,c,d\}$，包含 d ，所以能去掉。

3. 上一步的结果 $F=\{a \rightarrow b, bc \rightarrow d\}$，尝试减少左侧的属性

   1. 尝试将 $bc \rightarrow d$ 精简为 $c \rightarrow d$，得到 $G=\{a \rightarrow b, c \rightarrow d\}$，$\{c\}^+_F=\{c\}$，不包含 d，G 的依赖集相比 F 发生变化，所以不能精简。
   2. 尝试将 $bc \rightarrow d$ 精简为 $b \rightarrow d$，得到 $G=\{a \rightarrow b, b \rightarrow d\}$，$\{b\}^+_F=\{b\}$，不包含 d，G 的依赖集相比 F 发生变化，所以不能精简。
4. 没有需要合并的地方，最终结果为 $F=\{a \rightarrow b, bc \rightarrow d\}$

表格分解

规约化

把一张表分解为一张或者多张更小的表，但是在分解表的时候并不能经常保证蕴含了原来表的全部信息，造成了有损分解。

无损分解

判断分解成的两个表是不是无损分解, 就得根据表 T 的函数依赖集 F，检查两张表的标题交集的属性能否决定其中一张表的所有标题属性。

如何无损分解?

每个函数依赖左边的属性在老的核心的表中都出现，并决定了所有新表中的其他属性。

范式(NF, Normal Form)

超键

超键在关系中能够唯一标识元组的属性集，允许有多余属性。

给定表 T 和 它的一组函数依赖集 F，属性集 $X \subseteq Head(T)$，下面的描述等价

1. X 是 T 的超键
2. $X \rightarrow Head(T)$ 或者 $X^+_F \rightarrow Head(T)$

候选键

候选键同样可以唯一标识元组, 不允许有多余属性。

寻找候选键的方法

依次尝试去掉在 Head(T) 中的属性，若去掉后的属性集在 F 的闭包中包含了 T 的所有属性(可以决定 T 所有的属性)，就可以真的去掉了。

主属性(Primary Attribute)

候选键里的属性就是主属性。

1NF

关系型数据库的一张表中，每一列都不可再分割，即某一属性不能有多个值。

2NF

在 1NF 的基础上，消除了非主属性对于键（指候选键）的部分函数依赖。

判断方法

1. 找出表中所有非主属性
2. 查看是否存在有非主属性对键的部分函数依赖，若无则符合 2NF
3. 将数据表拆分成含有较少字段的表，修改为符合 2NF

3NF

在 2NF 的基础之上，消除了非主属性对于键的传递函数依赖。如果存在非主属性对于键的传递函数依赖，则不符合 3NF 的要求。

进行3NF的算法

给定通用表 T 和 FD 集 F 的情况下，该算法会生成 3NF 中的 T 的无损连接分解，并保留 F 的所有 FD。

1. 首先，将 F 替换成 F 的最小覆盖。
2. S = 空集

3. 对 F 中的所有 X->Y

   1. 如果对全部 Z 属于 S， $X \bigcup Y$ 不包含于 Z，则 $S = S \bigcup Head(X ⋃ Y)$

4. 如果对T的全部候选键K

   1. 对 Z 全部的 Z 属于 S，K 不包含于 Z
   2. 选择候选键 K，$S = S \bigcup Head(K)$

示例：

BCNF

在 3NF 基础上消除主属性对候选键的部分依赖和传递依赖。

BCNF 一定是 3NF

3NF 不一定是 BCNF

BCNF分解算法

1. 首先求出最小依赖集合
2. 找到候选键，合并成子集
3. 然后检查函数依赖左侧是不是都是候选键

将3NF分解为BCNF